Perpendicular Lines Form Right Angles

NOTE: The strategies for proofs of the theorems stated on this page are "discussed" only.
A "formal" proof would require that more than details be listed.

Two lines are perpendicular if and only if they form a right angle.

Perpendicular lines (or segments) really form four right angles, even if only i of the right angles is marked with a box.

The argument in a higher place is really a theorem which is discussed further downward on this page.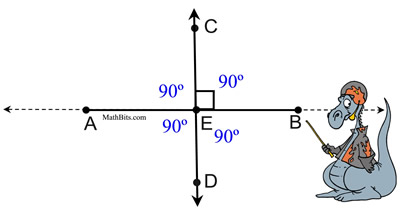

There are a couple of common sense concepts relating to perpendicular lines:

1. The shortest distance from a betoken to a line is the perpendicular altitude.

Any distance, other than the perpendicular distance, from point P to line m will get the hypotenuse of the right triangle. It is known that the hypotenuse of a right triangle is the longest side of the triangle.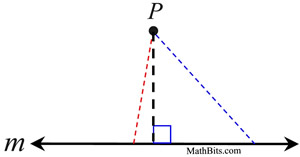

perp1

2. In a plane, through a indicate not on a line, in that location is one, and just one, perpendicular to the line.

If we assume there are two perpendiculars to line 1000 from betoken P, we volition create a triangle containing ii right angles (which is not possible). Our assumption of two perpendiculars from point P is not possible.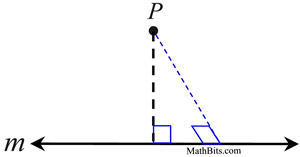

Perpendicular lines can likewise be connected to the concept of parallel lines:

3. In a plane, if a line is perpendicular to ane of two parallel lines, it is likewise perpendicular to the other line.

In the diagram at the correct, if k | | northward and t ⊥ m,
and so t ⊥ n.
The ii marked right angles are corresponding angles for parallel lines, and are therefore coinciding. Thus, a right angle too exists where line t intersects line northward.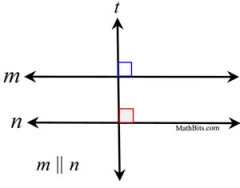

perp3

4. In a aeroplane, if two lines are perpendicular to the same line, the two lines are parallel.

In the diagram at the right, if t ⊥ grand and s ⊥ m,
then t | | due south.
Since t and s are each perpendicular to line thou, nosotros take 2 right angles where the intersections occur. Since all correct angles are coinciding, we have congruent respective angles which create parallel lines.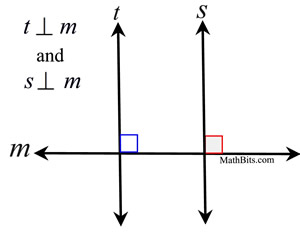

perp4

If two lines are perpendicular, they form four right angles.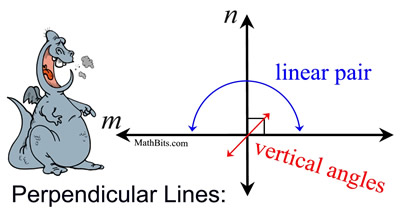

When two lines are perpendicular, at that place are 4 angles formed at the point of intersection. It makes no difference "where" yous label the "box", since all of the angles are right angles.

Past vertical angles, the two angles across from one some other are the same size (both 90º). By using a linear pair, the adjacent angles add to 180º, making any bending adjacent to the box another 90º bending.

If two lines intersect to form a linear pair of coinciding angles, then the lines are perpendicular.

When two adjacent angles form a linear pair, their non-shared sides grade a straight line (m). This tells united states that the measures of the ii angles will add together to 180º. If these ii angles also happen to be congruent (of equal measure), nosotros have two angles of the same size adding to 180º. Each angle will be 90º making m ⊥ n.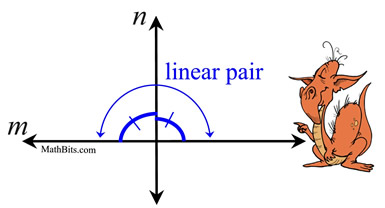

perporange

If two sides of two adjacent acute angles are perpendicular, then the angels are complementary.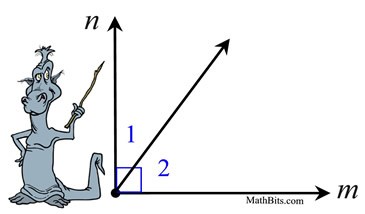

In the diagram at the left, <1 and <2 are acute next angles whose non-shared sides are perpendicular, grand ⊥ n. Since perpendiculars class right angles (90º), nosotros know the yard<1 + thousand<ii = 90º, making the angles complementary, by definition.

Note: The re-posting of materials (in role or whole) from this site to the Cyberspace is copyright violation
and is non considered "fair use" for educators. Delight read the "Terms of Use".